Question

The nth term of a geometric sequence is an = a1 • r n-1 , where a1 is the first term and r is the common ratio. Identify a1 and r for each geometric sequence. 1, 3, 9, 27, ... a = r = 8, 4, 2, 1, ... a = r = 4, -16, 64, -256, ... a =

Answer 1

1, 3, 9, 27, ...

a = 1

r = 3

8, 4, 2, 1, ...

a = 8

r = 1/2

4, -16, 64, -256, ...

a = 4

r = -4

Explanation:

Answer 2

1st sequence: a1 = 1, r = 3

2nd sequence: a1 = 8, r = 1/2

3rd sequence: a1 = 4, r = -4

Step-by-step explanation:

You can find a1 simply by looking at the first element of the sequence. This gives us that a1 is 1 in the first sequence, 8 in the second one, and 4 at the third one.

In order to find r, you can note that, if the nth term of the sequence is
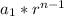`a_1 * r^(n-1)` , then the following term (the (n+1)th term) is
`a_1 * r^(n)` , which is obtained from the nth term by multiplying by r. This is true for any value of n, therefore

• a2 = r*a1
• a3 = r*a2
• a4 = r*a3

And so on. In order to obtain r we can observe by how much we are multiplying each term of the sequence to obtain the following one.

In the first sequence, we go from 1 to 3, then we go from 3 to 9, then we go from 9 to 27, and so on. We are multiplying each term by 3 to obtain the following one, thus r = 3.

In the second sequence, we go from 8 to 4, then to 2, then to 1, and so on. We are dividing by 2, or in other words, multiplying by 1/2. Therefore r = 1/2.

In the third sequence, we go from 4 to -16, then to 64, then to -256 and so on. In this case we multiply by a negative number, -4, which causes the sign to change when we go from one term to the next one. we conclude in this case that r = -4.

I hope this helps you!