Question

The gravitational force, F, between an object and the Earth is inversely proportional to the square of the distance from the object and the center of the Earth. If an astronaut weighs 186 pounds on the surface of the Earth, what will this astronaut weigh 4050 miles above the Earth? Assume that the radius of the Earth is 4000 miles.

Answer 1

45.95 pounds is the weight of the astronaut 4050 miles above the Earth.

Explanation:

The gravitational force F ∝
`(1)/(r^(2) )`

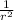
F =
`(k)/(r^(2))`

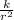
where r = Distance of the object from the center of the earth

and k = proportionality constant

For the astronaut weight = 186 pounds

186 =
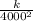`(k)/(4000^(2))` [ where radius of the Earth = 4000 miles]

k =
`186* 16* 10^(6)`

=
`2976* 10^(6)`

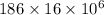
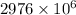
If the object is 4050 miles above the Earth then the weight of the object will be F =
`(2976* 10^(6) )/((4000+4050)^(2))`

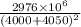
F =
`(2976* 10^(6) )/((8050)^(2))`

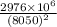
F =
`(2976* 10^(6) )/(64802500)`

=
`(2976000000)/(64802500)`

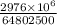
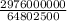
= 45.94 pounds

Therefore, 45.95 pounds is the weight of the astronaut 4050 miles above the Earth.