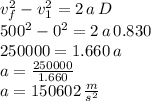Question

1.) A bullet leaves a rifle with a muzzle velocity of 500 m/s. While acceleration through the barrel

of the rifle, the bullet moves a distance of 0.830 m. Determine the acceleration of the bullet
(assume uniform acceleration )
a.) 125,500 m/s
b.) 250,500 m/s2
c.) 161,572 m/s
d.) 150,602 m/s2

Answer 1

`a=150602\,(m)/(s^2)` (Answer d)

Step-by-step explanation:

Since the problem doesn't include information on he time during which the bullet was accelerated, we can use the kinematic equation for motion under acceleration, that doesn't include time and relates initial and final velocities (
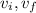`v_i, v_f`) with the acceleration exerted (
`a`), and the distance traveled (D):

`v_f^2-v_1^2= 2\,a\,D`

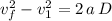
So, in this case, considering that the bullet starts at rest inside the muzzle (initial velocity
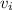`v_i` = zero), and reaches a final velocity
`v_f =` 500 m/s, and the distance the bullet travels inside the muzzle is 0.830 meters, we have the following equation from which we can solve for the acceleration:

`v_f^2-v_1^2= 2\,a\,D\\500^2-0^2=2\,a\,0.830\\250000=1.660\,a\\a=(250000)/(1.660) \\a=150602\,(m)/(s^2)`