Question

A box slides from rest down a frictionless ramp inclined at 34.0° with respect to the horizontal and is stopped at the bottom of the ramp by a spring with a spring constant of k = 3.50 104 N/m. If the box has a mass of 12.0 kg and slides 3.00 m from the point of release to the point where it comes to rest against the spring, determine the compression of the spring when the box comes to rest.

Answer 1

x = 0.105 meters

Step-by-step explanation:

It is given that,

A box slides from rest down a friction less ramp inclined at 34.0° with respect to the horizontal,
`\theta=34^(\circ)`

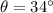
Spring constant of the spring,
`k=3.5* 10^4\ N/m`

Mass of the box, m = 12 kg

Th box slides 3 m from the point of release to the point where it comes to rest against the spring. We need to find the compression of the spring when the box comes to rest.

Let h is the height of the incline,

`h=sin(34)* 3=1.67\ m`

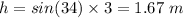
Using the conservation of energy in case of spring,

`(1)/(2)kx^2=mgh`

`x=\sqrt{(2mgh)/(k)}`

`x=\sqrt{(2* 12* 9.8* 1.67)/(3.5* 10^4)}`

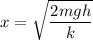
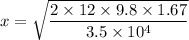
x = 0.105 meters

So, the compression of the spring is 0.105 meters. Hence, this is the required solution.