Question

A 22kg box slides down a 30.0 degree incline. If there is no friction, what is the acceleration of the box?

Answer 1

Acceleration of the box is 4.9 m/s².

Step-by-step explanation:

The free body diagram is shown below.

The weight of the body can be resolved into two mutually perpendicular components as shown. The force responsible for sliding motion of the box along the incline is due to
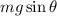`mg\sin \theta` acting along the incline.

Therefore, as per Newton's second law of motion,

Net force =
`mass* acceleration`

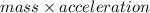
Now, net force acting along the incline is only
`mg\sin \theta`

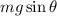
Therefore,

`mg\sin \theta=ma\\a=g\sin \theta`

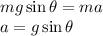
Now,
`g=9.8\textrm{ and } \theta = 30`

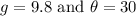
Therefore, the acceleration of the box is given as:

`a=9.8* \sin(30)=9.8* 0.5=4.9\textrm{ }m/s^(2)`

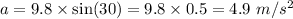
Acceleration of the box is 4.9 m/s².