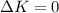Answer:
Part a)
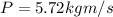
Part b)
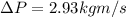
Part c)

Part d)
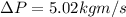
Part e)
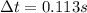
Part f)
Step-by-step explanation:
As we know that initial velocity of the ball is given as
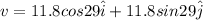
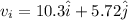
Now final velocity of the system is given as
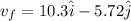
Part a)
now magnitude of initial momentum is given as
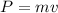
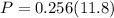
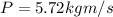
Part b)
Change in momentum is given as
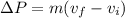
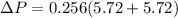
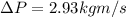
Part c)
As we know that average force is defined as the rate of change in momentum
so here we have



Part d)
Magnitude of change in momentum is given as
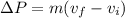
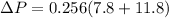
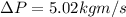
Part e)
As we know that in 2nd case the force is same as the initial force
so we will have
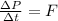
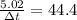
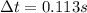
Part f)
Since this is elastic collision so change in kinetic energy must be ZERO