Question

15 POINT, need this answered ASAP

Write an equation of an ellipse in standard form with the center at the origin and with the given characteristics. vertex at (-3,0) and co-vertex (0,2)
a. x^2/9+y^2/4=1
b. x^2/4+y^2/9=1
c. x^2/3+y^2/9=1
d. x^2/2+y^2/3=1

Answer 1

Option A

The equation of ellipse in standard form is
`(x^(2))/(9)+(y^(2))/(4)=1`

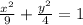
Solution:

Given, We have to write an equation of an ellipse in standard form with the center at the origin

Given that vertex at (-3,0) and co-vertex (0,2)

The standard form of an ellipse is
`(x^(2))/(a^(2))+(y^(2))/(b^(2))=1`

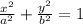
where a is x- intercept and b is y – intercept.

We have vertex (-3, 0) and (0, 2) from these we can say that, x – intercept is – 3 and y – intercept is 2 . As we know that intercepts are the respective values when other variables becomes 0.

Now, let us find our ellipse equation:

`\begin{array}{l}{\rightarrow (x^(2))/((-3)^(2))+(y^(2))/(2^(2))=1} \\\\ {\rightarrow (x^(2))/(9)+(y^(2))/(4)=1}\end{array}`

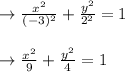
Hence, the standard form equation is
`(x^(2))/(9)+(y^(2))/(4)=1`

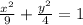
Thus option A is correct