Answer:
Explanation:
1) slope = 3 ; y-intercept = 1
y = mx + b
y = 3x + 1
0 = 3x + 1 -y
-1 = 3x - y
ANS: 3x - y = -1
2) Passing through (0,2), slope = -4
y - y₁ = m(x -x₁)
y - 2 = -4(x - 0)
y - 2 = -4x
4x + y - 2 = 0
Ans: 4x + y = 2
3)Passing through (-1,3) and (1,1)
Slope =
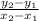
![= (1-3)/(1-[-1])\\\\= (-2)/(1+1)\\\\= (-2)/(2)\\\\= - 1](https://img.qammunity.org/2022/formulas/mathematics/college/kjifetbozbxzahd9v78boo0ng2oat7t7kh.png)
m= -1 ; (-1 , 3)
y - y₁ = m(x -x₁)
y - 3 = (-1)(x - [-1] )
y -3 = (-1)(x +1 )
y - 3 = -x - 1
x + y -3 = -1
x +y = -1 + 3
Ans: x + y = 2
4) Passing through (1,3), slope = 1/2
y - y₁ = m(x -x₁)

Multiply the equation by 2
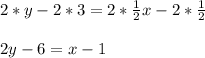
2y - 6 +1 = x
2y - 5 = x
-5 = x - 2y
Ans: x - 2y = -5
5) Passing through (1/2,1) and (4,2)
Slope =

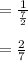
m = 2/7 ; (4 , 2)
y - y₁ = m(x -x₁)
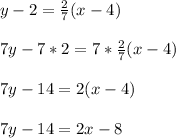
7y - 14 + 8 = 2x
7y - 6 = 2x
Ans: 2x - 7y = -6