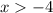1 Answer

Ganeshragav · Answer 1 · 2020-11-27T11:13:01+0000

For this case we have the following inequality:

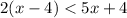
2 (x-4) <5x + 4

We apply distributive property on the left side of inequality:

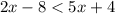
2x-8 <5x + 4

We subtract 5x on both sides of the inequality:

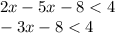
$2x-5x-8 <4\\-3x-8 <4$

We add 8 to both of the inequality:

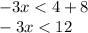
$-3x <4 + 8\\-3x <12$

We divide between 3 on both sides of the inequality:

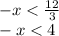
$-x <\frac {12} {3}\\-x <4$

We multiply by -1 on both sides taking into account that the sense of inequality changes.

x> -4

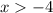
Answer:

Please log in or register to add a comment.