Answer:
(A) 5.22 m/s
(B) 637.98 j
Step-by-step explanation:
from the question we are given the following
mass of the skier (m) = 62 kg
initial velocity of the skier (U1) =6.5 m/s
length of the rough path (s) = 3.5 m
coefficient of kinetic friction (
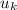 ) = 0.3
) = 0.3
height of the hill (y) = 2.5 m
acceleration due to gravity (g) = 9.8 m/
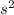
final velocity (v) =?
(a) To solve this problem we would split the motion of the skier into two phases:
phase 1 would be from when he starts to when he gets to the icy slope
phase 2 would be down the icy slope
we would be applying the equation below
work done due to gravity + work done due to friction = K2 - K1
where K1 and K2 are the kinetic energies
kinetic energy =
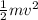
work done due to gravity = m x g x height of the slope
work done due friction =
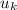 x m x g x s
x m x g x s
Phase 1:
when the skier moves across the rough patch the the work done due to gravity is 0 since he moves horizontally and perpendicular to the gravitational force. Therefore the equation now becomes
work done due to friction = K2 - K1
-(0.3 x 62 x 9.8 x 3.5 =
![(1)/(2) 62 x [tex]U_(2)](https://img.qammunity.org/2020/formulas/physics/high-school/1rfw2e1jikrpwscqb7dnfpxq2kjl9iwt4u.png) ^{2}[/tex]) -
^{2}[/tex]) -
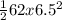
-637.98 =
![31[tex]U_(2)](https://img.qammunity.org/2020/formulas/physics/high-school/6h25x6ajflsoy5mbui9eyq9a5adhj224tv.png) ^{2}[/tex] - 1309.75
^{2}[/tex] - 1309.75
U_{2} = 4.66 m/s
Phase 2
when the skier moves down the hill on a friction free snow, work is only done by gravity. therefore the equation becomes
work done due to gravity = K3 - K2
62 x 9.8 x 2.5 =
![(1)/(2) 62 x [tex]U_(3)](https://img.qammunity.org/2020/formulas/physics/high-school/e9x0x99y9ruz3u8t755vcpyrmrwkujwfrb.png) ^{2}[/tex]) -
^{2}[/tex]) -
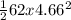
1519 = 31
 ^{2} + 673.18
^{2} + 673.18
U_{3} = 5.22 m/s
at the end of the slope the skier's velocity is 5.22 m/s
(B) the internal energy generated while crossing the rough path is the same as the work done due to friction = 637.98 j
(this is because internal energy is the manifestation of work done by non-conservative forces, and frictional force is a non-conservative force).