Answer:
Frederick collects the an amount of $4813.24 at the age of 18 out of which $2000 was the beginning amount.
Explanation:
We are given the following information in the question:
Amount = 2000
Interest rate = 5%
The money is compounded annually or yearly.
Time = 18 years
Compound interest =
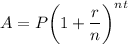
where P is the principal amount, r is the interest rate, t is the time in years and n is the number of compounding in a year.
Since, the money is compounded yearly we put n = 1.
Putting all the values, we get,
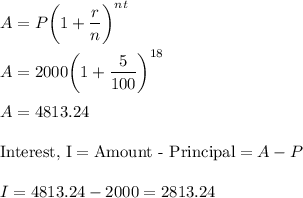
Thus, Frederick collects the an amount of $4813.24 at the age of 18 out of which $2000 was the beginning amount.