Question

(3) Finding Dory Coral Reef communities are home to one-quarter of all marine plants and animals worldwide. These reef support large fisheries by providing breeding grounds and safe havens for young fish of many species. Coral reefs are seawalls (protecting shorelines from tides, storm-surges, and hurricanes as well as produce the limestone and sand of which beaches are made), Marine scientists say that a tenth of the world’s reef systems have been destroyed in recent times. At current rates of loss, almost three-quarters of the reefs could be gone in 30 years. A particular lab studies corals and the diseases that affect them. Dr. Drew Harvell and his lab sampled sea fans at 19 randomly selected reefs along the Yucatan peninsula and diagnosed whether the animals (the sea fans) were affected by aspergillosis1 . In specimens collected at a depth of 40 feet at the Las Redes Reef in Akumal, Mexico, scientists found that 52% of the 104 sampled sea fans were infected with aspergillosis.

(a) What are the mean (proportion, p) and standard deviation of the sampling distribution of the sample proportion (mean (p) and sepˆ) of infected sea fans? What should the distribution look like (think of the definition of CLT)?

(b) What is probability that the sample proportion of infected sea fans is less than 50% (that is find P(ˆp < .5))?

(c) What is probability that the sample proportion of infected sea fans is between 40 and 60%?

Answer 1

a)

Mean

p = 0.52

Standard deviation

s = 0.049

b) 34.16%

c) 94.16%

Explanation:

(a) What are the mean (proportion, p) and standard deviation of the sampling distribution of the sample proportion (mean (p) and sepˆ) of infected sea fans? What should the distribution look like (think of the definition of CLT)?

The sample size is

n = 104

the proportion is

p = 0.52

As a rule of thumb, if both np ≥ 15 and n(1-p) ≥ 15, we can approximate this discrete binomial distribution with the continuous Normal distribution, and due to the Central Limit Theorem, the larger the sample size, the better the approximation to the Normal.

The approximation should look like a Normal curve with this parameters:

Mean

p = 0.52

Standard deviation

`\bf s=\sqrt{(p(1-p))/(104)}=\sqrt{(0.52*0.48)/(104)}=0.049`

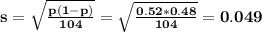
(b) What is probability that the sample proportion of infected sea fans is less than 50% (that is find P(ˆp < 0.5))?

Here, we want the area under the Normal curve described in a) to the left of 0.5 (See picture 1)

We can do it directly with a calculator or a spreadsheet.

In Excel use

NORMDIST(0.5,0.52,0.049,1)

In OpenOffice Calc use

NORMDIST(0.5;0.52;0.049;1)

and we obtain an area of 0.3416 or 34.16%

(c) What is probability that the sample proportion of infected sea fans is between 40 and 60%?

Here we want the area under the Normal curve with the parameters established in (a) between the values 0.4 and 0.6 (See picture 2)

In Excel use

NORMDIST(0.6,0.52,0.049,1) - NORMDIST(0.4,0.52,0.049,1)

In OpenOffice Calc use

NORMDIST(0.6;0.52;0.049;1) - NORMDIST(0.4;0.52;0.049;1)

and we obtain an area(probability) of 0.9416 or 94.16%