Question

How many computers must the AB Computer Company sell to break even? Let x be the number of computers.

Cost Function:c(x)=145+1/4x

Revenue Function: r(x)=15x


Enter in the number of computers only.

Answer 1

116 computers.

Explanation:

We have been given cost function and revenue function for AB Computer Company. We are asked to find the break-even point.

We know that break-even is a point, when total cost is equal to total revenue that is company make no profit or no loss.

To find break-even, we will equate cost function with revenue function and solve for x as:

`c(x)=145+(1)/(4)x`

`r(x)=1.5x`

`145+(1)/(4)x=1.5x`

`145+0.25x=1.5x`

`1.5x=145+0.25x`

`1.5x-0.25x=145+0.25x-0.25x`

`1.25x=145`

`(1.25x)/(1.25)=(145)/(1.25)`

`x=116`

Therefore, the AB Computer Company must sell 116 computers to break-even.

Answer 2

Answer:
`10\ computers`

Explanation:

To solve this exercise it is important to remember the cost must be equal to the revenue in order to break even.

In this case, given the Cost function:

`c(x)=145+(1)/(4)x`

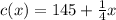
And given the Revenue function:

`r(x)=15x`

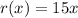
We must equate them:

`c(x)=r(x)\\\\145+(1)/(4)x=15x`

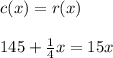
Since "x" represents the number of computers that AB Computer Company must sell to break even, we have to solve for "x" in order to find its value.

Then:

`145+(1)/(4)x=15x\\\\145=15x-(1)/(4)x\\\\145=14.75x\\\\x=9.83\\\\x\approx10`

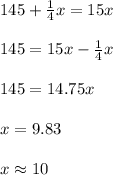
Therefore, the AB Computer Company must sell 10 computers to break even.