Answer:
Answer:
The graph will be
 2 units away from the origin on positive
2 units away from the origin on positive
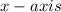 and three units upward from the origin towards
and three units upward from the origin towards
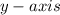 .
.
Step-by-step explanation:
Here is a graph attached with it.
To graph
 we know that positive
we know that positive
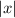 is a
is a
 shaped from the origin.
shaped from the origin.
Key points:
- To move rightward there must be a negative inside the parentheses.
- And to move upward we must have positive
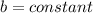 .
.
If we have to move towards
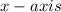 then we must have negative inside it.
then we must have negative inside it.
And if we have to move upward in
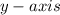 positive we must have positive constant value.
positive we must have positive constant value.
So the graph will be three units upward and two units rightward with a V-shaped ray.