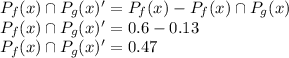Question

The US Energy Department states that 60% of all US households have ceiling fans. In addition, 29% of all US households have an outdoor grill. Suppose 13% of all US households have both a ceiling fan and an outdoor grill. A US household is randomly selected.

a) What is the probability that the household has a ceiling fan or an outdoor grill?
b) What is the probability that the household has neither a ceiling fan nor an outdoor grill?
c) What is the probability that the household does not have a ceiling fan and has an outdoor grill?
d) What is the probability that the household does have a ceiling fan and does not have an outdoor grill?

Answer 1

For the development of this problem we will use the basic concept of Probability and relation of sets.

Our values are:

`P(Grill)= P_g(x)= 0.29`

`P(fans)=P_f(x)= 0.6`

`P(both)=P_b(x)= 0.13`

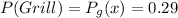
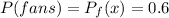
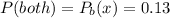
PART A ) What is the probability that the household has a ceiling fan or an outdoor grill?

`P_f(x) \cup P_g(x)= P_f(x) +P_g(x)-P_b(x)`

`P_f(x) \cup P_g(x)= 0.6+0.29-0.13`

`P_f(x) \cup P_g(x)= 0.76`

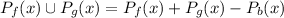
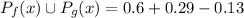
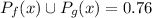
PART B) What is the probability that the household has neither a ceiling fan nor an outdoor grill?

`P_f(x)' \\ot\cup P_g(x)'=1-P_f(x) \cup P_g(x)\\P_f(x)' \\ot\cup P_g(x)'=1-0.76\\P_f(x)' \\ot\cup P_g(x)'= 0.24`

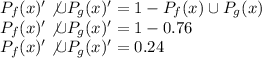
PART c) What is the probability that the household does not have a ceiling fan and does have an outdoor grill?

`P_f(x)' \cap P_g(x)=P_g(x)-P_f(x) \cap P_g(x)\\P_f(x)' \cap P_g(x)= 0.29-0.13\\P_f(x)' \cap P_g(x)=0.16`

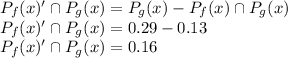
PART D) What is the probability that the household does have a ceiling fan and does not have an outdoor grill?

`P_f(x) \cap P_g(x)' = P_f(x)-P_f(x) \cap P_g(x)\\P_f(x) \cap P_g(x)' =0.6-0.13\\P_f(x) \cap P_g(x)' =0.47`