Answer:
The correct answer is option A) 55⁰.
Step-by-step explanation:
As we know that the sum of interior angles of triangle is 180⁰.
So, adding all the given sides and subtracting to 180⁰, to find the value of x.
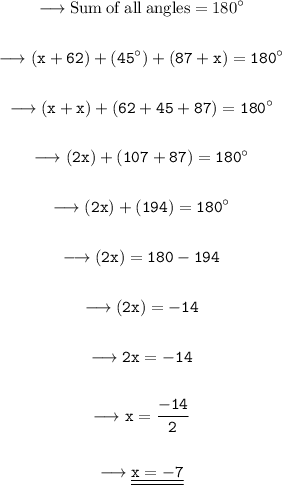
Hence, the value of x is -7.

Now, we know the value of x. So, calculating the measurement of angle A.
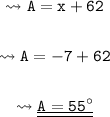
Hence, the measurement of angle A is 55⁰.
