You break even if you spend exactly as much as you gain. In other words, if the cost and the revenue are the same:
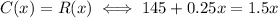
Subtract 0.25 from both sides:

Divide both sides by 1.25:
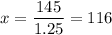
So, they must sell 116 computers to break even. If they sell less, they'll lose money. If they sell more, they'll start making profit.