Answer:
The time to reach 1000 mg is 7 hours
Explanation:
Given as :
The rate at which bacteria growing = 2.34% per hour
The initial amount of bacteria = 850 mg
The final amount of bacteria = 1000 mg
Let The time period fro bacteria growing = T hours
Now, Final value = Initial value ×
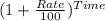
Or, 1000 mg = 850 mg ×

Or,
 =
=

Or, 1.1764 =

Or, 1.1764 =
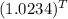
Or, Taking log both side
log(1.1764) = log (
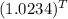 )
)
Or, 0.07055 = T × 0.01004 (
 )
)
∴ T = 7.026 hour or T ≈ 7 hours
Hence The time to reach 1000 mg is 7 hours Answer