Question

The first card selected from a standard 52-card deck was a king. It is

returned to the deck, what is the probability that a king will be drawn on
the second selection?
A. 1/4 or 0.25
B. 1/13, or 0.077
C. 12/13, or 0.923
D. 1/3 or 0.33
None of the above​

Answer 1

Option B

The probability of getting a king card is 1/13 or 0.077, so option B is correct.

Solution:

Given that , The first card selected from a standard 52-card deck was a king.

It is returned to the deck

We have to find what is the probability that a king will be drawn on the second selection?

Now, the first selected card is king and it is returned to the deck.

So it has no effect on the second selection card.

Then, we have to find probability to get a king

`\text { probability }=\frac{\text { favourable outcomes for a king }}{\text { total possible outcomes }}=\frac{4 \text { king cards }}{52 \text { cards in total }}=(4)/(52)=(1)/(13)`

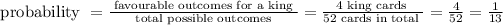
Hence, the probability of getting a king card is 1/13 or 0.077