Answer:
The speed of the jet in still air is 415 mph and the speed of the wind is 19 mph
Explanation:
we know that
The speed is equal to divide the distance by the time
Let
x -----> the speed of the wind in miles per hour
y ----> the speed of the jet in still air in miles per hour
we know that
With a tailwind
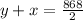
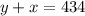 ----> equation A
----> equation A
With a headwind
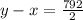
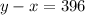 ----> equation B
----> equation B
solve the system of equations A and B by elimination
Adds equation A and equation B
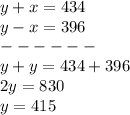
Find the value of x
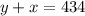
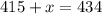

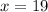
therefore
The speed of the jet in still air is 415 mph and the speed of the wind is 19 mph