Answer:
The sum of the 10 terms of geometric series is 4092
Step-by-step explanation:
Given in the question, the series that will be formed is in Geometric Progression (GP) is the common ratio is mentioned here
According to GP, the sum of a series is given by the formula;
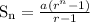
Then, according to question,
a is given as 4, n is given as 10 and r is given as 2.
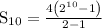
=
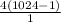
= 4(1023)= 4092
Therefore, the sum of the 10 terms of geometric series is 4092