Question

Find 3 consecutive even num big ears where the product of the smaller two numbers is 52 less than the square of the largest number

Answer 1

Smallest consecutive number = 6

Second consecutive number = 8

Largest consecutive number = 10

Explanation:

Let us assume the first even number = k

Then the next consecutive even number (k +2)

And the third consecutive even number = (k+2) + 2= k + 4

Now, Product of two smaller number = k (k+2)

Also, the square of the largest number =
`(k+4)^2`

Now, according to the question:

`k(k+2) = (k+4)^2 - 52`

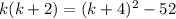
Now, using ALGEBRAIC IDENTITY:
`(a+b)^2 = a^2 + b^2  + 2ab`

`k(k+2) = (k+4)^2 - 52  \implies  k ^2  + 2k = k^2 + 8k + 16 -52\\or, 2k  -  8k = 16 - 52  \implies -6k = -36\\\implies k = 36/6= 6`

or, k = 6

Hence, the smallest consecutive number = k = 6

Second consecutive number = k + 2 = 6 + 2 = 8

Largest consecutive number = k + 4 = 6 + 4 = 10

Hence, 6 , 8 and 10 are the required numbers.