Answer:
t = 60.3 minutes.
Explanation:
The function
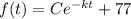 ........ (1)
........ (1)
Now, at t = 0, f(0) = 150 = C + 77
⇒ C = 73
So, the function (1) becomes
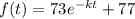 ......... (2)
......... (2)
Now, it is given that at t = 10 minutes, f(10) = 120 degree.
Therefore, from equation (2),
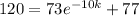
⇒
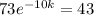
⇒
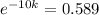
Now, taking ln both sides we get -10k (ln e) =ln (0.589)
⇒ k = 0.0529
Therefore, the equation (2) becomes
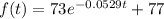 ......(3)
......(3)
Now, putting f(t) = 80 degree, we have fro equation (3),

⇒
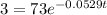
⇒
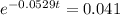
Taking ln both sides we get, -0.0529t = - 3.19, ⇒ t = 60.3 minutes. (Answer)