Question

1. y = x2 + 8x + 15
Find the zeros of the function by rewriting the function in intercept form

Answer 1

The zeros of given function
`y=x^(2)+8 x+15` is – 5 and – 3

Solution:

`\text { Given, equation is } y=x^(2)+8 x+15`

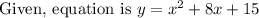
We have to find the zeros of the function by rewriting the function in intercept form.

By using intercept form, we can put value of y as to obtain zeros of function

We know that, intercept form of above equation is
`x^(2)+8 x+15=0`

`\text { Splitting } 8 x \text { as }(5+3) x \text { and } 15 \text { as } 5 * 3`

`\begin{array}{l}{\rightarrow x^(2)+(5+3) x+5 * 3=0} \\\\ {\rightarrow x^(2)+5 x+3 x+5 * 3=0}\end{array}`

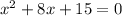
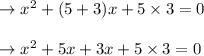
Taking “x” as common from first two terms and “3” as common from last two terms

x (x + 5) + 3(x + 5) = 0

(x + 5)(x + 3) = 0

Equating to 0 we get,

x + 5 = 0 or x + 3 = 0

x = - 5 or – 3

Hence, the zeroes of the given function are – 5 and – 3