Question

A car moving at 46 km/h skids 14 m with locked brakes. How far will the car skid with locked brakes at 92 km/h? Assume that energy loss is due only to sliding friction. Answer in units of m.

Answer 1

at 92 km/h the car will skid 56 meters

Step-by-step explanation:

Notice that the only force acting to stop the car is the force of friction which we assume is the same in both cases because we deal with the same car under similar pavement/tire conditions. Therefore the negative acceleration that stops the car must be the same in both cases. we don't know that acceleration but can use the letter a
`a` to represent its magnitude in our equations.

We will also use the subindex "1" to represent the physical quantities associated with the equations of motion for the first case (car moving at 46 km/h) such that
`v_1, \, t_1, x_1` represent the velocity, time to stop, and distance traveled under the negatively accelerated motion in this first case.

Similarly, we represent with subindex "2" the physical quantities associated with the second case (car moving at 92 km/h) and for which we need to find the distance covered under negatively accelerated motion.

Equations of motion for the first case (car breaking - negative acceleration) from an initial velocity
`v_1` to rest (zero velocity). Lets start with the equation for the acceleration:
`-a=(0-v_1)/(t_1) \\-a=(-v_1)/(t_1)\\t_1=(-v_1)/(-a) \\t_1=(v_1)/(a)`

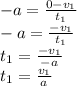
We use this expression for the stopping time in the other equation of motion that involves the distance
`x_1` covered in the stopping process:

`x_1=v_1*t_1-(1)/(2) a*t_1^2\\x_1=v_1((v_1)/(a)) -(1)/(2) a*((v_1)/(a)) ^2\\x_1=(v_1^2)/(a) -(1)/(2) (v_1^2)/(a) \\x_1=(1)/(2) (v_1^2)/(a)`

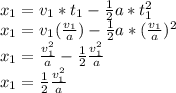
We can extract from here the expression for the magnitude of the acceleration that, since it is the same as for the second case, we can use in the new equations of motion associated with it:

`a=(v_1^2)/(2*x_1)`

For the second case we do a similar study considering that the car goes from velocity
`v_2` to rest, in a time
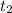`t_2`, and covering a distance
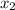`x_2` (what we need to find):

`-a=(0-v_2)/(t_2) \\-a=(-v_2)/(t_2)\\t_2=(-v_2)/(-a) \\t_2=(v_2)/(a)`

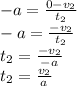
And in the equation for the distance covered:

`x_2=v_2*t_2-(1)/(2) a*t_2^2\\x_2=v_2((v_2)/(a)) -(1)/(2) a*((v_2)/(a)) ^2\\x_1=(v_2^2)/(a) -(1)/(2) (v_2^2)/(a) \\x_2=(1)/(2) (v_2^2)/(a)`

And we now use the expression for the magnitude of the acceleration from the first case (for which we know the distance covered) to replace it and find the new distance to full stop:

`x_2=(1)/(2) (v_2^2)/(a)\\x_2= (1)/(2)(v_2^2\,2\,x_1)/(v_1^2) \\x_2=(v_2^2)/(v_1^2) x_1`

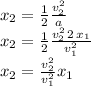
We now just replace the values for the velocities and for the breaking distance for case 1. Notice that since we are dividing velocities that have the same units they cancel out and we don;t need to worry about converting units to the SI system. The answer for the breaking distance in case 2 will come in the same units as the breaking distance for case 1 (that is in meters). We proceed now to use the numerical values to get our answer:

`x_2=(v_2^2)/(v_1^2) x_1\\x_2=(92^2)/(46^2) 14\\x_2=56`

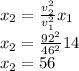
Then, the car travelling at 92 km/h will skid 56 meters