Question

Suppose that the system will work if components 1 and 2 are both working, or if components 3 and 4 are both working, or if components 1, 3, and 5 are all working. Let W be the event that the system will work. Specify all the outcomes in W.

Answer 1

`A \ system \ is \ composed \ o f \ 5 \ components \ , \ e ach \ of \ which \ is \ either \ working \ or`
`failed. \ Consider \ an \ experiment \ that \ consists \ of \ observing \ the \ status \ of \ each`
`component \ . and \ let \ the \ outcome \ of \ the \ experiment \ be \ given \ by \ the \ vector`
`(x1,x2,x3, x4, x5), \ where \ xi \ is \ equal \ to \ 1\ if \ component \ i \ is \ working \ and \ is \\ equal \ to \ 0 \ if \ component \ i \ is \ failed.`

`(a) \ How \ many \ outcomes \ are \ in \ the \ sample \ space \ of \ this \ experiment?`

`(b) \ Suppose \ that \ the \ system \ wil l \ work \ if \ components \ 1 \ and \ 2 \ are \ both \\ working, or \ if \ components \ 3 \ and \ 4 \ are \ both \ working, \ or \ if \ components \ 1, \ 3, \\ and \ 5 \ are \ all \ working. \ Let \ W \ be \ the \ event \ that \ the \ system \ will \ work. \ Specify \\ all \ the \ outcomes \ i n \ W.`

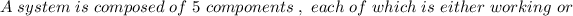
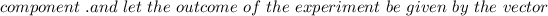
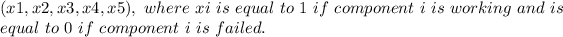
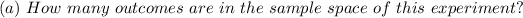
Answer:

Explanation:

From the given information:

We learned that it is possible that all entities can be in one of two states i.e. 0 or 1. Thus, all 5 entities can either be 0 or 1 (2 states).

∴

Number of outcomes = 2 × 2 × 2 × 2 × 2

= 2⁵

= 32

b)

All the outcomes of W = {(1, 1, x₃, x₄, x₅) (x₁, x₂, 1, 1, x₅) (1, x₂, 1, x₄, 1)}