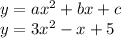Question

Find the equation of the parabola that passes through the points:
(0,5) (1,7) (-2,19)

Answer 1

y= 3x^2 - x+5

Explanation:

hope that helps

Answer 2

`y=3x^(2) -x+5`

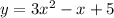
Explanation:

The general form of a parabola is

`y=ax^(2) +bx+c`

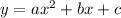
Now, we have three points, where each of them gives values for (x,y). We can use them to create a system of three equations with three unknown variables

`5=c\\7=a(1)^(2) +b(1)+c\\19=a(-2)^(2) +b(-2)+c`

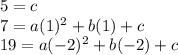
Then, we replace the value of
`c` in the second and third equation to find create an equation with only two variables

`7=a+b+5\\19=4a-2b+5`

`2=a+b\\14=4a-2b`

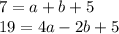
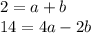
Then, we multiply the first equation by 2, and sum both equations

`4=2a+2b\\14=4a-2b`

`18=6a\\a=(18)/(6)\\ a=3`

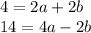
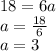
Finally, we use this value to find
`b`

`2=a+b\\2=3+b\\b=2-3\\b=-1`

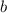
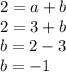
Therefore, the equation of the parabola is

`y=ax^(2) +bx+c\\y=3x^(2) -x+5`