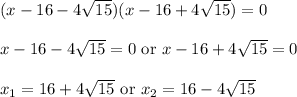Question

Solving Rational and Radical Equations: Mastery Test

Arrange the steps to solve the equation v1+3-V2r-1=-2.
Simplify to obtain the final radical term on one side of the equation.
Raise both sides of the equation to the power of 2.
Apply the Zero Product Rule.
Use the quadratic formula to find the values of x.
Simplify to get a quadratic equation.
Raise both sides of the equation to the power of 2 again plato​

Answer 1

1 step: Raise both sides of the equation to the power of 2.

2 step: Simplify to obtain the final radical term on one side of the equation.

3 step: Raise both sides of the equation to the power of 2 again.

4 step: Simplify to get a quadratic equation.

5 step: Use the quadratic formula to find the values of x.

6 step: Apply the Zero Product Rule.

Explanation:

Given the equation

`√(x+3)-√(2x-1)=-2`

1 step: Raise both sides of the equation to the power of 2.

`(√(x+3)-√(2x-1))^2=(-2)^2\\ \\(√(x+3))^2-2√(x+3)√(2x-1)+(√(2x-1))^2=4\\ \\x+3-2√(x+3)√(2x-1)+2x-1=4`

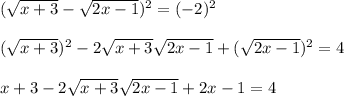
2 step: Simplify to obtain the final radical term on one side of the equation.

`x+3-2√(x+3)√(2x-1)+2x-1=4\\ \\3x+2-2√(x+3)√(2x-1)=4\\ \\-2√(x+3)√(2x-1)=4-3x-2\\ \\-2√(x+3)√(2x-1)=2-3x`

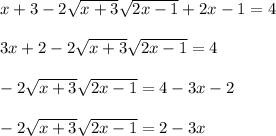
3 step: Raise both sides of the equation to the power of 2 again.

`(-2√(x+3)√(2x-1))^2=(2-3x)^2\\ \\4(x+3)(2x-1)=(2-3x)^2`

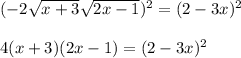
4 step: Simplify to get a quadratic equation.

`4(2x^2-x+6x-3)=2^2-2\cdot 2\cdot 3x+(3x)^2\\ \\8x^2-4x+24x-12=4-12x+9x^2\\ \\8x^2+20x-12-4+12x-9x^2=0\\ \\-x^2+32x-16=0\\ \\x^2-32x+16=0`

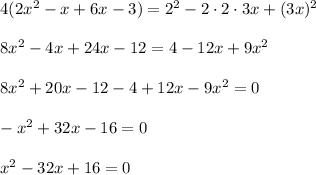
5 step: Use the quadratic formula to find the values of x.

`D=(-32)^2-4\cdot 1\cdot 16=1,024-64=960\\ \\x_(1,2)=(-(-32)\pm √(960))/(2\cdot 1)=(32\pm 8√(15))/(2)=16\pm 4√(15)`

Then the equation is

`(x-16-4√(15))(x-16+4√(15))=0`

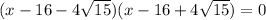
6 step: Apply the Zero Product Rule.

`(x-16-4√(15))(x-16+4√(15))=0\\ \\x-16-4√(15)=0\text{ or }x-16+4√(15)=0\\ \\x_1=16+4√(15)\text{ or }x_2=16-4√(15)`