Question

a painter uses a rope to raise a 3.55 kg bucket at a constant speed. How much force does the rope exert on the bucket?​

Answer 1

34.79 N is correct for acellus

Answer 2

The rope exerts 34.79 N force on the bucket.

Step-by-step explanation:

Given:

Mass of the bucket,
`m=3.55\textrm{ kg}`

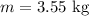
Acceleration due to gravity,
`g=9.8\textrm{ }m/s^(2)`

Speed of the bucket is constant.

Since the speed of the bucket is not changing, there will be no acceleration produced and thus net acceleration of the bucket is 0 m/s².

Now, the forces acting on the bucket are:

1. Upward tension force by the rope,
`T`.

2. Downward weight of the bucket,
`W=mg`.

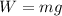As the acceleration of the bucket is zero, therefore, upward force is equal to downward force.

So,
`T=mg=3.55* 9.8=34.79\textrm{ N}`

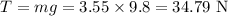
Hence, the tension force on the bucket by the rope is 34.79 N.