Question

Find the point slope form and slope intercept form, indicate the slope and y-int:

1) 3x+4y=-12


2) -2x-3y=6

Answer 1

1) The point slope form and slope intercept form of 3x + 4y = -12 are
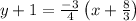`y+1=(-3)/(4)\left(x+(8)/(3)\right)` and
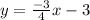`y= (-3)/(4)x-3` respectively

And slope is
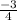`(-3)/(4)` and y -intercept is -3

2) The point slope form and slope intercept form of -2x - 3y = 6 are
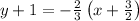`y+1=-(2)/(3)\left(x+(3)/(2)\right)` and
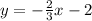`y=-(2)/(3) x-2` respectively

And slope is
`(-2)/(3)` and y-intercept is -2

Solution:

Given, two equations are 3x + 4y = - 12 ⇒ (1) and – 2x – 3y = 6 ⇒ (2)

We have to find the point slope form and slope intercept form, and have to indicate the slope and y-intercept.

The point slope form is given as:

`y-y_(1)=m\left(x-x_(1)\right)`

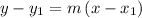
Where "m" is the slope of the line

The slope-intercept form is given as:

y = mx + c

Where "c" is the y-intercept

1) Solving 3x + 4y = -12

Given equation is 3x + 4y = -12

On rearranging the terms, we get,

`\begin{array}{l}{4 y=-3 x-12} \\\\ {\rightarrow y=(-3)/(4)-3}\end{array}`

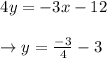
Hence the slope intercept form is
`y=(-3)/(4)-3`

`\text { where slope is }-(3)/(4) \text { and } y-\text { intercept is }-3`

`\text { Point slope form i.e. } y-y_(1)=m\left(x-x_(1)\right)`

`\begin{array}{l}{3 x+4 y=-12} \\\\ {\rightarrow 4 y=-3 x-12} \\\\ {\rightarrow y=(-3)/(4) x-3} \\\\ {\rightarrow y=(-3)/(4) x-2-1} \\\\ {\rightarrow y+1=(-3)/(4)\left(x+(8)/(3)\right)}\end{array}`

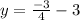
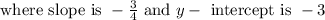
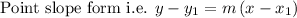
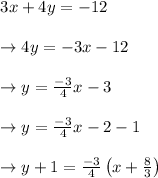
2) Solving -2x – 3y = 6

Slope intercept form is given as:

`-2 x-3 y=6 \rightarrow-3 y=2 x+6 \\\\\rightarrow y=-(2)/(3) x-2`

`\text { where slope is }-(2)/(3) \text { and } y-\text { intercept is }-2`

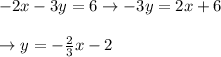
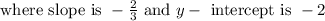
Point slope form is given as:

`\begin{array}{l}{-2 x-3 y=6 \rightarrow-3 y=2 x+6} \\\\ {\rightarrow y=-(2)/(3) x-2} \\\\ {\rightarrow y=-(2)/(3) x-1-1} \\\\ {\quad \rightarrow y+1=-(2)/(3)\left(x+(3)/(2)\right)}\end{array}`

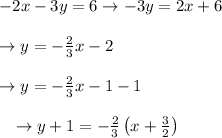
Hence the required slope and y-intercept are found