Question

If sin θ = 3/8 and θ is in the second quadrant, find values of all 5 other trigonometric functions of θ

Answer 1

Hence The other five trigonometric function as :

CosФ =
`(√(73))/(8)`

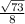
TanФ =
`(3)/(√(73))`

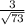
SecФ =
`(8)/(√(73))`

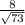
CotФ =
`(√(73))/(3)`

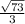
Explanation:

Given as :

sin Ф =
`(3)/(8)`

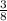
∵ sin Ф =
`(perpendicular)/(hypotenuse)`

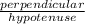
So,
`(perpendicular)/(hypotenuse)` =
`(3)/(8)`

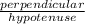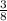
Then from Pythagorean theorem

Hypotenuse² = Perpendicular² + Base²

So, Base² = Hypotenuse² - Perpendicular²

Or, Base² = 8² + 3² = 64 + 9 = 73

∴ Base = √73

So, CosФ =
`(Base)/(hypotenuse)`

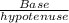
CosФ =
`(√(73))/(8)`

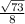
TanФ =
`(perpendicular)/(Base)`

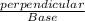
TanФ =
`(3)/(√(73))`

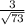
SecФ =
`(hypotenuse)/(base)`

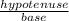
SecФ =
`(8)/(√(73))`

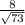
CotФ =
`(Base)/(Perpendicular)`

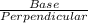
CotФ =
`(√(73))/(3)`

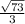
CosecФ =
`(hypotenuse)/(perpendicular)`

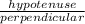
CosecФ =
`(8)/(3)`

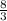
Hence The other five trigonometric function as :

CosФ =
`(√(73))/(8)`

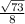
TanФ =
`(3)/(√(73))`

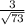
SecФ =
`(8)/(√(73))`

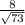
CotФ =
`(√(73))/(3)`

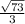
CosecФ =
`(8)/(3)` Answer