Question

Two satellites A and B orbit the Earth in the same plane. Their masses are 5 m and 7 m, respectively, and their radii 4 r and 7 r, respectively What is the ratio of their orbital speeds

Answer 1

The ratio of their orbital speeds are 5:4.

Step-by-step explanation:

Given that,

Mass of A = 5 m

Mass of B = 7 m

Radius of A = 4 r

Radius of B = 7 r

The orbital speed of satellite A,

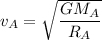`v_(A)=\sqrt{(GM_(A))/(R_(A))}`......(I)

The orbital speed of satellite B,

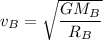`v_(B)=\sqrt{(GM_(B))/(R_(B))}`......(I)

We need to calculate the ratio of their orbital speeds

Using equation (I) and (II)

`(v_(A))/(v_(B))=\sqrt{((GM_(A))/(R_(A)))/((GM_(B))/(R_(B)))}`

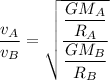
Put the value into the formula

`(v_(A))/(v_(B))=\sqrt{(G*5m*7r)/(G*7m*4r)}`

`(v_(A))/(v_(B))=(5)/(4)`

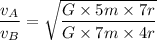
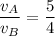
Hence, The ratio of their orbital speeds are 5:4.