Question

Which situation could NOT represent a proportional relationship?

Question 1 options:

The weight in x weeks of a puppy that gains 2 pounds per week if it starting weight is 8 pounds.


The cost of purchasing p pounds of bananas for $0.55 per pound.


The number of gallons of water in x barrels with 50 gallons of water in each barrel


The amount an employee who makes $9.25 per hour earns in h hours

Answer 1

The weight in x weeks of a puppy that gains 2 pounds per week if it starting weight is 8 pounds.

Explanation:

Given:

A proportional relationship is one in which one variable varies directly with the other. Let the dependent variable be y and independent variable be y.

If y is directly proportional to x, then,

`y=kx`, where, k is a constant of proportionality.

Now, let us check each option and try to express a relationship between them.

Option 1:

The weight in
`x` weeks of a puppy that gains 2 pounds per week if it starting weight is 8 pounds.

Let the weight be represented by
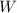`W`. Initial weight is 8 pounds.

Weight gain per week is 2 pounds. So, weight gain in
`x` weeks is
`2x`.

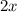Therefore, total weight is,
`W=8+2x`

This is a linear relationship but not a proportional relationship as it is not of the form
`y=kx`. So, option 1 could NOT represent a proportional relationship.

Option 2:

Cost of purchasing 1 pound of bananas is $ 0.55. So, cost of purchasing
`p` pounds of bananas will be
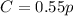`C=0.55p`. It is of the form
`y=kx`. So, it represents a proportional relationship.

Option 3:

Number of gallons of water in 1 barrel is 50. So, number of gallons in
`x` barrels will be
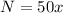`N=50x`. It is of the form
`y=kx`. So, it represents a proportional relationship.

Option 4:

Amount earned by an employee in 1 hour is $ 9.25. So, amount earned in
`h` hours will be
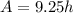`A=9.25h`. It is of the form
`y=kx`. So, it represents a proportional relationship.