Question

The volume of a cylindrical container

is 1 gallon. If the dimensions are
dilated by a scale factor of 3/4, what is
the volume of the new container?

Answer 1

A.
`(3)/(4)\textrm{ gal}`

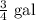
Explanation:

Given:

Volume of the cylindrical container before dilation,
`V_(i)=1\textrm{ gal}`

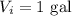
Scale factor of the dilation,
`SF=(3)/(4)`

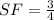
Therefore, the volume of the dilated cylinder is given as:

`V_(f)=SF* V_(i)`

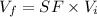
Plug in 1 gal for
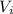`V_(i)` and
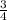`(3)/(4)` for SF. Solve for
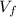`V_(f)`. This gives,

`V_(f)=(3)/(4)* 1\\V_(f)=(3)/(4)\textrm{ gal}`

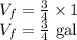
Therefore, the volume of the dilated cylinder is
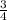`(3)/(4)` gallons.