Answer:
A number line from negative 7 to 7 in increments of 1. Two points, one at negative 6 and one at negative 2.
Explanation:
Given:
The equation is:
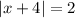
For an absolute function, if
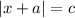 , where,
, where,
 and
and
 are some real numbers, then,
are some real numbers, then,
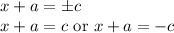
Therefore, the above equation can be expressed as:
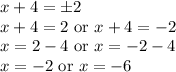
Therefore, on a number line, the values of
 are -6 and -2.
are -6 and -2.