Answer:
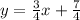
Explanation:
The slope of straight line PR where P(2,3) and R(5,-1) are two vertices of triangle PQR will be =
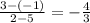
Therefore, the slope of the altitude passing through Q(-1,1) will be
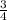 {Since, the product of slopes of two perpendicular straight line is -1}
{Since, the product of slopes of two perpendicular straight line is -1}
So, equation of the altitude is
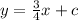 where c is a constant.
where c is a constant.
Now, putting x = -1 and y = 1 in the above equation we get
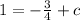
⇒
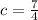
Therefore, the equation of the altitude is
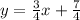 (Answer)
(Answer)