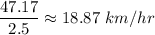Question

Two boats leave the same place at the same time. The first boat heads due north at 10 kilometers per hour. The second boat heads due west at 16 kilometers per hour. After 2.5 hours, how fast is the distance between the boats increasing

Answer 1

After 2.5 hours, the distance between the two boats is not increasing or decreasing. It remains constant at approximately 18.87 km/h.

Step-by-step explanation:

To solve this problem, we can use the concept of relative velocity. The first boat is moving north at a speed of 10 km/h, and the second boat is moving west at a speed of 16 km/h. We can use the Pythagorean theorem to find the distance between the two boats:

1. Distance = √((10 km/h)^2 + (16 km/h)^2) = √(100 km^2/h^2 + 256 km^2/h^2) = √356 km/h ≈ 18.87 km/h

Now, to find how fast the distance between the two boats is increasing, we can differentiate the distance formula with respect to time:

1. d(Distance)/dt = (d(√(100 km^2/h^2 + 256 km^2/h^2))/dt = (1/2) * (2*100 km/h * (d(100 km/h)/dt) + 2*256 km/h * (d(256 km/h)/dt))/(√(100 km^2/h^2 + 256 km^2/h^2)) = (100 km/h * (d(100 km/h)/dt) + 256 km/h * (d(256 km/h)/dt))/(√(100 km^2/h^2 + 256 km^2/h^2))
2. Since we are given that the boats have been traveling for 2.5 hours, we can substitute the given values into the equation and calculate the rate of change of the distance:
3. d(Distance)/dt = (100 km/h * 0 + 256 km/h * 0)/(√(100 km^2/h^2 + 256 km^2/h^2)) = 0 km/h

Therefore, after 2.5 hours, the distance between the two boats is not increasing or decreasing. It remains constant at approximately 18.87 km/h.

Answer 2

18.87 km/hr

Step-by-step explanation:

First boat is heading North with a speed of 10 km/hr.

Second boat is heading West with a speed of 16 km/hr.

Time for which they move = 2.5 hours

To find:

The speed at which the distance is increasing between the two boats.

Solution:

Let the situation be represented by the attached diagram.

Their initial position is represented by point O from where they move towards point A and point B respectively.

`Distance = Speed * Time`

`Distance\ OA = 10 * 2.5 = 25\ km`

`Distance\ OB = 16 * 2.5 = 40\ km`

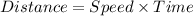
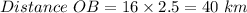
We can use Pythagorean Theorem to find the distance AB.

AB is the hypotenuse of the right angled
`\triangle AOB`.

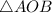According to Pythagorean theorem:

`\text{Hypotenuse}^(2) = \text{Base}^(2) + \text{Perpendicular}^(2)\\\Rightarrow AB^(2) = OA^(2) + OB^(2)\\\Rightarrow AB^2 = 25^2 + 40^2\\\Rightarrow AB^2 = 2225^2\\\Rightarrow AB^2 \approx 47.17\ km`

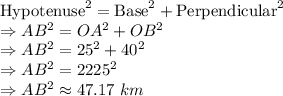
The speed at which distance is increasing between the two boats is given as:

`(47.17)/(2.5) \approx 18.87\ km/hr`