Question

A research report claims that 20% of all individuals use Firefox to browse the web. A software company is trying to determine if the proportion of their users who use Firefox is significantly different from 0.2. In a sample of 200 of their users, 36 users stated that they used Firefox. Using this data, conduct the appropriate hypothesis test using a 0.01 level of significance. a) What are the appropriate hypotheses?

a)H0: p = 0.2 versus Ha: p < 0.2
b)H0: p = 0.2 versus Ha: p ≠ 0.2
c)H0: μ = 0.2 versus Ha: μ > 0.2
d)H0: p = 0.2 versus Ha: p > 0.2
b) What is the test statistic?
Give your answer to four decimal places.
c) What is the P-value for the test? Give your answer to four decimal places.
d) What is the appropriate conclusion?
a)Fail to reject the claim that the Firefox proportion is 0.2 because the P-value is smaller than 0.01.
b)Conclude that the Firefox proportion is not 0.2 because the P-value is smaller than 0.01.

Answer 1

Answer: (a) H0: p = 0.2 versus Ha: p ≠ 0.2

(b) The test statistics is z- statistics = - 0.7071

(c) The P - value = 0.4796

(d) Conclude that the Firefox proportion is 0.2 because the P-value is larger than 0.01.

Step-by-step explanation: The test is a 2 - sided test , using the Z- statistics:

Sample mean = 36/200 = 0.18

Population mean = 0.2

Therefore:

Z =
`\frac{0.18 - 0.2}{\sqrt{(0.2(1-0.2))/(200) } }`

=
`\frac{- 0.02}{\sqrt{(0.2(0.8))/(200) } }`

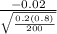
= - 0.7071

Therefore , the test statistics = - 0.7071

(c) The P - value for the 2 - sided test implies

2 * P ( Z > /-0.7071/ ) = 0.4796

(d) Conclude that the Firefox proportion is 0.2 because the P- Value is larger than 0.01