Question

When the oxide of generic metal M is heated at 25C, only a negligible amount of M is produced. MO2(s) <---> M(s)+O2(g) delta G = 288.5 kJ/mol

1.) When the reaction is coupled to the conversion of graphite to carbon dioxide, it becomes spontaneous. What is the chemical equation of this coupled process? Show that the reaction is in equilibrium, include physical states, and represent graphite as C(S) _________________________________
2.) What is the thermodynamic equilibrium constant for the coupled reaction? K = ????

Answer 1

1.
`MO_2(s)+C(s)<-->CO_2(g)+M(s)`

2.
`K=3.57x10^(18)`

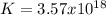
Step-by-step explanation:

Hello,

1.) By coupling the given reaction with the formation of carbon dioxide, one states the total reaction as:

`MO_2(s)<-->M(s)+O_2(g)\\C(s)+O_2(g)<-->CO_2(g)`

____________________________________

`MO_2(s)+C(s)<-->CO_2(g)+M(s)`

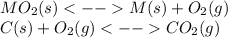
2.) Now, since we know that the Gibbs free energy for the decomposition of the metal is 288.5kJ/mol and the Gibbs free energy for the formation of carbon dioxide has a value of −394.39kJ/mol, the total Gibbs free energy for this process is:

Δ
`G^o=288.5kJ/mol-394.39kJ/mol=-105.89kJ/mol`

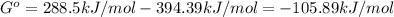
So the equilibrium constant is:

`K=exp(-(DeltaG^0)/(RT) )\\K=exp(-(-105890J/mol)/(8.314J/molK*298.15K) )\\K=3.57x10^(18)`

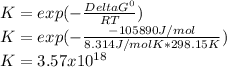
Best regards.