Answer:
The pair of solutions are
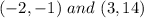
Explanation:
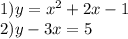
Solving for
 in equation 2.
in equation 2.
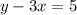
Adding
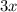 both sides.
both sides.
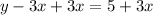
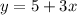
Substituting value of
 in equation 1.
in equation 1.
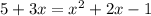
Simplifying it further. Subtracting
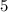 from both sides.
from both sides.
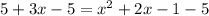
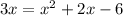
Subtracting
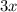 both sides.
both sides.
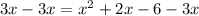
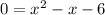
Now we have a quadratic equation to solve.
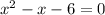
Solving quadratic by factor method.
Splitting the middle term into two terms
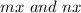 such that
such that
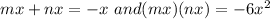
By factoring 6 we can get the terms.
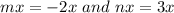 As we know
As we know
![[2x-3x=-x \ and\ (2x)(-3x)=-6x^2]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/2hfswxqvigblqnwhle8h2fuvjaeib2p38f.png)
So, the equation would be
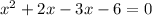
Now, we factor in pairs.
Taking
 as common factor from first two terms and taking
as common factor from first two terms and taking
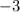 common from last two terms.
common from last two terms.
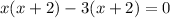
Taking
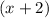 as common factor from the whole.
as common factor from the whole.
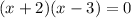
The roots can be written as:
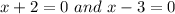
Solving for
 from the above we get
from the above we get
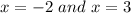
Plugging the values of
 in the equation
in the equation
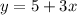
When

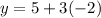
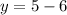
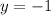
So
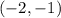 is one solution.
is one solution.
When
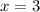
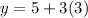
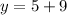
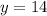
So
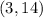 is another solution.
is another solution.