Answer:
a) 14M
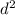
Step-by-step explanation:
a)The inertia of a particle moving in a circular axis is given by,
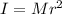
I = Moment of inertia
M = mass of the particle
r = perpendicular distance from axis of rotation.
And by adding moment of inertia of each particle we can come to the moment of inertia of the system.
I = M
 +M
+M
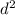 +M
+M
 +M
+M
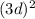
= 14M
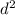
b) Your question is incomplete but I'll write how to find the minimum force required to give a system given angular acceleration.
Minimum force is found when applied from the furthest point to the axis of rotation in the system.
, by τ = Fr, whereτ = torque , F = Force , = perpendicular distance from axis of rotation.
For minimum force r = 3d
And also τ = Iα where I = Moment of inertia and α = angular acceleration
By combining the two equations you get minimum force as,
F = Iα/r
F' = 14M
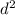 α/3d
α/3d
= 14Mαd/3