Question

The moment of inertia for a set of point masses is given by the equation, I=∑nimir2i. What is the moment of inertia for a frame of four point masses positioned at the corners of an essentially massless rigid frame if the frame rotates around one side like a door rotates on its hinges. Each mass is 2.00 kg and the sides of the square frame all have a length of 0.68 m.

Answer 1

`I=1.84\ kg.m^2`

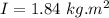
Step-by-step explanation:

It is given that,

Mass of each mass, m = 2 kg

Side of the square frame, l = 0.68 m

It is clearly written in the question that the four point masses positioned at the corners of an essentially massless rigid frame if the frame rotates around one side like a door rotates on its hinges. Let ABCD are the vertices of square and AB acts like a door.

The moment of inertia for a set of point masses is given by :

`I=\sum n_im_ir_i^2`

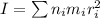
So,

`I=I_A+I_B+I_C+I_D`

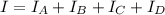
The sum of inertia at A and B is 0 because l = 0

`I=0+0+ml^2+ml^2`

`I=2ml^2`

`I=2* 2\ kg* (0.68\ m)^2`

`I=1.84\ kg.m^2`

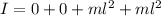
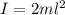
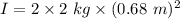
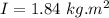
So,the moment of inertia for a frame of four point masses positioned at the corners is
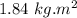`1.84\ kg.m^2`. Hence, this is the required solution.