Answer:
Around 27.2 years later
Explanation:
This is compound decline problem. We use the formula:
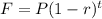
Where
F is future amount (100)
P is present amount (229)
r is the rate of decrease (3% means 3/100 = 0.03)
t is the time in years (which we want to find)
So, lets substitute and solve:
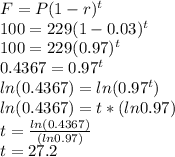
So, around 27.2 years later, the population would reach 100