Question

Given: △ABC, m∠A=60°, m∠C=45°, AB=9 Find: Perimeter of △ABC, Area of △ABC do not rationlize

Answer 1

p = 32.32; A = 47.91

Explanation:

1. Calculate ∠B

∠A + ∠B + ∠C = 180°

60° + ∠B + 45° = 180°

∠B + 105° = 180°

∠B = 75°

2. Find sides BC and AC

We can use the Law of Sines

`(\sin A)/(BC) = (\sin B)/(AC) = (\sin C)/(AB)`

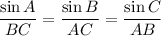
(i) Find BC

`(\sin 75^(\circ))/(AC) = (\sin 45^(\circ))/(9)\\\\(0.8660)/(BC) = (0.7071)/(9)\\\\BC = 9 * (0.8661)/(0.7071) = 11.02`

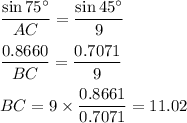
(ii) Find AC

`(\sin 75^(\circ))/(AC) = (\sin 45^(\circ))/(9)\\\\(0.9659)/(AC) = (0.7071)/(9)\\\\BC = 9 * (0.9659)/(0.7071) = 12.29`

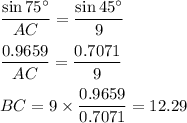
3. Find the perimeter

p = AB + AC + BC = 9 + 12.29 + 11.02 = 32.32

4. Find the area of the triangle

A general formula for the area of a triangle is

A = ½ab sinC

If we use ∠A, the formula becomes

A = ½ × 9 × 12.29 × sin60° = 55.30 × 0.8660 = 47.91