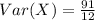Answer:
The value of
 .
.
The value of
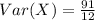 .
.
Explanation:
Consider the provided information.
The number of hours between successive train arrivals at the station is uniformly distributed on (0, 1). Passengers arrive according to a Poisson process with rate 7 per hour.
Let X denote the number of people who get on the next train.
Part (A)
Here, X = N(T), N(t) ∼ Poisson(λt), and λ = 7
Therefore, E(N(T)|T) = λT
Now find E(X) as shown below
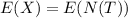

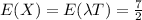
Hence, the value of
 .
.
Part (B)
Now we need to find VAR[X]
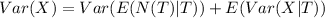
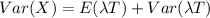
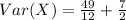
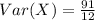
Hence, the value of