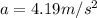Question

The first stage of a space vehicle consumed fuel and oxidizer at the rate of 1.75 x 104 kg/s, with an exhaust speed of 2.40 x 103 m/s. Find the acceleration (in m/s2) of the vehicle just as it lifted off the launch pad on the Earth, if the vehicle's initial mass was 3.00 x 106 kg. (Note: You must include the force of gravity to solve the problem.)

Answer 1

`a=4.19 m/s^(2)`

Step-by-step explanation:

In order to solve this problem, we must first draw a free body diagram of the situation. (See attached picture)

from this diagram, we can do the following sum of forces:

`\sum F=ma`

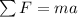
where m is the mass of the rocket and a is its acceleration.

`F_(e)-mg=ma`

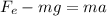
where
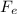`F_(e)` is the force of exhaust. We can solve this for the acceleration, so we get:

`a=(F_(e)-mg)/(m)`

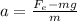
we can find the force of exhaust by using the momentum formula:

Ft=mv

so we can solve this for the force:

`F_(e)=(mv)/(t)`

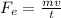
the problem already tells us what m/t is equal to, so we can directly substitute:

`F_(e)=(1.75x10^(4)kg/s)(2.40x10^3m/s)`

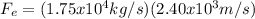
which yields:

`F_(e)=42x10^6 N`

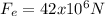
So we can now substitute:

`a=(42x10^6N-(3x10^6kg)(9.81m/s^(2)))/(3x10^6kg)`

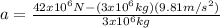
so:

`a=4.19 m/s^(2)`