Question

Car A is traveling at 18.0 m/s and car B at 25.0 m/s. Car A is 300 m behind car B when the driver of car A accelerates his car with an acceleration of 1.80 m/s2. How long does it take car A to overtake car B

Answer 1

car A reaches and immediately overtakes the car B at 22.56 s.

Step-by-step explanation:

After car A accelerate at 1.8 m/s2, it travels a distance x(A) and car B will have travels a distance x(B), let's recall that the initial distance between them is 300 m, so we have:

`x_(A)=300+x_(B)`

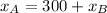
Now, we can rewrite this equation in terms of speed and time

`V_(iA)t+(1)/(2)at^(2)=300+V_(iB)t`

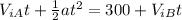
Where:

V(iA) is the initial speed of car A

V(iB) is the initial speed of car B

t is the time when car A reaches the car B

a is the acceleration

`18t+(1)/(2)1.8t^(2)=300+25t`

`0.9t^(2)-7t-300=0`

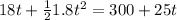
Solving this quadratic equation for t, and taking just the positive value, we will have:

t=22.56 s

Therefore, car A reaches and immediately overtakes the car B at 22.56 s.

I hope it helps you!