Answer :
(2) The % of Cl in the sample is 56.8 %
(3) The concentration of Cl in ppm for the river water is 33.2 mg/L
Explanation :
Part 2 :
First we have to calculate the moles of
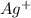
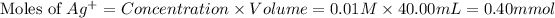
The chemical reaction will be:
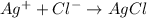
From the reaction we conclude that,
As, 1 mole of
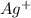 react with 1 mole of
react with 1 mole of

So, 0.40 mmol of
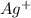 react with 0.40 mmol of
react with 0.40 mmol of

Now we have to calculate the moles of
 ion in 250 mL.
ion in 250 mL.
As, 25.00 mL contains moles of
 ion = 0.40 mmol
ion = 0.40 mmol
So, 250.0 mL contains moles of
 ion =
ion =
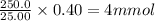
Now we have to calculate the mass of
 ion.
ion.
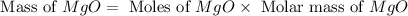
Molar mass of
 ion = 35.5 g/mole
ion = 35.5 g/mole
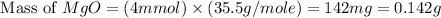
Now we have to calculate the % of Cl in the sample.

Hence, the % of Cl in the sample is 56.8 %
Part 3 :
First we have to calculate the moles of
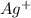

The chemical reaction will be:
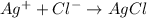
From the reaction we conclude that,
As, 1 mole of
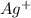 react with 1 mole of
react with 1 mole of

So, 0.0935 mmol of
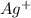 react with 0.0935 mmol of
react with 0.0935 mmol of

Now we have to calculate the mass of
 ion.
ion.
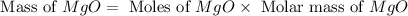
Molar mass of
 ion = 35.5 g/mole
ion = 35.5 g/mole
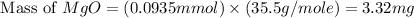
Now we have to calculate the concentration of Cl in ppm.
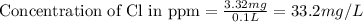
Hence, the concentration of Cl in ppm for the river water is 33.2 mg/L