Answer: d).0264
Explanation:
Given : It is known that screws produced by a certain company will b defective with probability .01 independently of each other.
The company sells the screws in packages of 25 and offers a money back guarantee that at most 1 of the 25 is defective.
Let x be the binomial variable that represents the defective screws having parameter p= 0.01 and n= 25
For using Poisson approximation for binomial distribution
Mean =
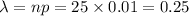
Poisson distribution formula :
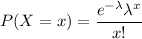
Now, the probability that the company must replace a package is
=Probability that package has more than 1 defectives
=
![P(x>1)=1-(P(x\leq1))\\\\=1-[P(x=0)+P(x=1)]\\\\=1-[e^(-0.25)\cdot(0.25^0)/(0!)+e^(-0.25)\cdot(0.25^1)/(1!)]\\\\=1-0.9736=0.0264](https://img.qammunity.org/2020/formulas/mathematics/college/fs3afsuzxj3rwcvxj5fw109jgxgvk4v0ib.png)
Hence, the required probability is 0.0264