Question

In a massive-star supernova explosion, a stellar core collapses to form a neutron star roughly 10 kilometers in radius. The gravitational potential energy released in such a collapse is approximately equal to G M2/R, where M is the mass of the neutron star, R is its radius, and G is the gravitational constant. Using this formula, estimate the amount of gravitational potential energy released in a massive -star supernova explosion. How does it compare with the amount of energy radiated by the Sun during its entire main-sequence lifetime?

Answer 1

The concept used to solve this problem is gravitational potential Energy.

The equation is given by,

`U=(GM^2)/(R)`

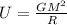
Where U is the gravitational potential energy

M is the mass of object

R is radius (10000m)

G is the unviersal gravitational constant
`(6.67*10^(-11)m^3/kgs^2)`

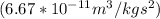
We know that the mass of neutron star is 1.4 times the mass of the sun.

It is known that the mass of sun is
`2*10^(30)Kg`

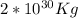
Replacing the values in our equation we have:

`U= ((6.67*10^(-11))(1.4*(2*10^(30))))/(10000)`

`U= 5.2*10^(46)J`

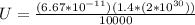
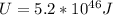
Therefore the energy released in a massive-star supernova explosion is
`5.2*10^(46)J`

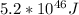
To estimate the second point we know that the Total Energy by the Sun is

`E_(sun)=8*10^(35)J`

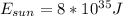
We can calculate the ratio between a supernova explosion and our entire main-sequence lifetime energy of the sun.

`U' = (U)/(E_(sun))`

`U' = (5.2*10^(46)J)/(8*10^(35)J)`

`U' = 6.5*10^(10)`

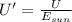
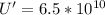
Therefore the amount of energy radiated by a supernova explosion is around
`10^(10)` times more than the entire main-sequence lifetime energy of the sun.